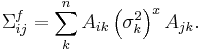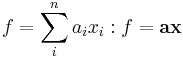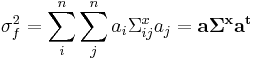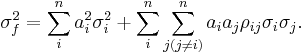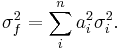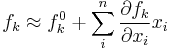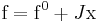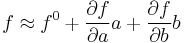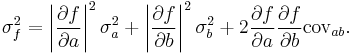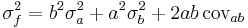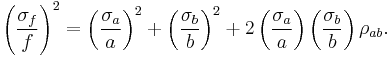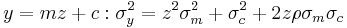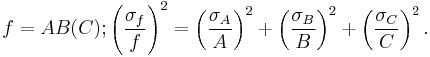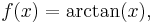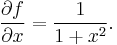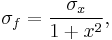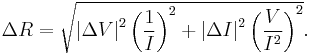Propagation of uncertainty

In statistics, propagation of error (or propagation of uncertainty) is the effect of variables' uncertainties (or errors) on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations (e.g., instrument precision) which propagate to the combination of variables in the function.

The uncertainty is usually defined by the absolute error. Uncertainties can also be defined by the relative error (Δx)/x, which is usually written as a percentage.

Most commonly the error on a quantity, Δx, is given as the standard deviation, σ. Standard deviation is the positive square root of variance, σ². The value of a quantity and its error are often expressed as x ± Δx. If the statistical probability distribution of the variable is known or can be assumed, it is possible to derive confidence limits to describe the region within which the true value of the variable may be found. For example, the 68% confidence limits for a one dimensional variable belonging to a normal distribution are ± one standard deviation from the value, that is, there is a 68% probability that the true value lies in the region x ± σ. Note that the percentage 68% is approximate as the exact percentage that corresponds to one standard deviation is slightly larger than this.

If the variables are correlated, then covariance must be taken into account.

1 Linear combinations
2 Non-linear combinations
- 2.1 Example
3 Caveats and warnings
4 Example formulas
5 Partial derivatives
- 5.1 Example calculation: Inverse tangent function
- 5.2 Example application: Resistance measurement
6 See also
7 Notes
8 References
9 External links

Linear combinations

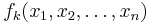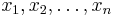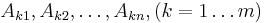Let $f_k(x_1,x_2,\dots,x_n)$ be a set of m functions which are linear combinations of $n$ variables $x_1,x_2,\dots,x_n$ with combination coefficients $A_{k1},A_{k2},\dots,A_{kn}, (k=1\dots m)$ .

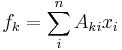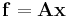
$f_k=\sum_i^n A_{ki} x_i$ or $\mathbf{f}=\mathbf{Ax}\,$

and let the variance-covariance matrix on x be denoted by 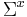$\Sigma^x\,$ .

$\Sigma^x = \begin{pmatrix} \sigma^2_1 & \text{cov}_{12} & \text{cov}_{13} & \cdots \\ \text{cov}_{12} & \sigma^2_2 & \text{cov}_{23} & \cdots\\ \text{cov}_{13} & \text{cov}_{23} & \sigma^2_3 & \cdots \\ \vdots & \vdots & \vdots & \ddots \\ \end{pmatrix}$

Then, the variance-covariance matrix 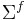$\Sigma^f\,$ , of f is given by

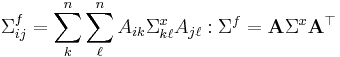$\Sigma^f_{ij}= \sum_k^n \sum_\ell^n A_{ik} \Sigma^x_{k\ell} A_{j\ell}: \Sigma^f=\mathbf{A} \Sigma^x \mathbf{A}^\top$ .

This is the most general expression for the propagation of error from one set of variables onto another. When the errors on x are un-correlated the general expression simplifies to

$\Sigma^f_{ij}= \sum_k^n A_{ik} \left(\sigma^2_k \right)^x A_{jk}.$

Note that even though the errors on x may be un-correlated, their errors on f are always correlated.

The general expressions for a single function, f, are a little simpler.

$f=\sum_i^n a_i x_i: f=\mathbf {a x}\,$

$\sigma^2_f= \sum_i^n \sum_j^n a_i \Sigma^x_{ij} a_j= \mathbf{a \Sigma^x a^t}$

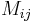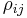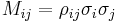Each covariance term, $M_{ij}$ can be expressed in terms of the correlation coefficient $\rho_{ij}\,$ by $M_{ij}=\rho_{ij}\sigma_i\sigma_j\,$ , so that an alternative expression for the variance of f is

$\sigma^2_f= \sum_i^n a_i^2\sigma^2_i%2B\sum_i^n \sum_{j (j \ne i)}^n a_i a_j\rho_{ij} \sigma_i\sigma_j.$

In the case that the variables x are uncorrelated this simplifies further to

$\sigma^{2}_{f}= \sum_i^n a_{i}^{2}\sigma^{2}_{i}.$

Non-linear combinations

When f is a set of non-linear combination of the variables x, it must usually be linearized by approximation to a first-order Taylor series expansion, though in some cases, exact formulas can be derived that do not depend on the expansion.^[1]

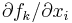$f_k \approx f^0_k%2B \sum_i^n \frac{\partial f_k}{\partial {x_i}} x_i$

where $\partial f_k/\partial x_i$ denotes the partial derivative of f_k with respect to the i-th variable. Or in matrix notation,

$\mathrm{f} = \mathrm{f}^0 %2B J \mathrm{x}\,$

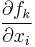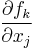where J is the Jacobian matrix. Since f⁰_k is a constant it does not contribute to the error on f. Therefore, the propagation of error follows the linear case, above, but replacing the linear coefficients, A_ik and A_jk by the partial derivatives, $\frac{\partial f_k}{\partial x_i}$ and $\frac{\partial f_k}{\partial x_j}$ . In matrix notation,

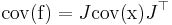$\operatorname{cov}(\mathrm{f}) = J \operatorname{cov}(\mathrm{x}) J^\top$ .[1]

That is, the Jacobian of the function is used to transform the rows and columns of the covariance of the argument.

Example

Any non-linear function, f(a,b), of two variables, a and b, can be expanded as

$f\approx f^0%2B\frac{\partial f}{\partial a}a%2B\frac{\partial f}{\partial b}b$

hence:

$\sigma^2_f=\left| \frac{\partial f}{\partial a}\right| ^2\sigma^2_a%2B\left| \frac{\partial f}{\partial b}\right|^2\sigma^2_b%2B2\frac{\partial f}{\partial a}\frac{\partial f}{\partial b}\text{cov}_{ab}.$

In the particular case that 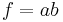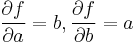$f=ab\!$ , $\frac{\partial f}{\partial a}=b, \frac{\partial f}{\partial b}=a$ . Then

$\sigma^2_f=b^2\sigma^2_a%2Ba^2 \sigma_b^2%2B2ab\,\text{cov}_{ab}$

$\left(\frac{\sigma_f}{f}\right)^2=\left(\frac{\sigma_a}{a}\right)^2%2B\left(\frac{\sigma_b}{b}\right)^2%2B2\left(\frac{\sigma_a}{a}\right)\left(\frac{\sigma_b}{b}\right)\rho_{ab}.$

Caveats and warnings

Error estimates for non-linear functions are biased on account of using a truncated series expansion. The extent of this bias depends on the nature of the function. For example, the bias on the error calculated for log x increases as x increases since the expansion to 1+x is a good approximation only when x is small.

In data-fitting applications it is often possible to assume that measurements errors are uncorrelated. Nevertheless, parameters derived from these measurements, such as least-squares parameters, will be correlated. For example, in linear regression, the errors on slope and intercept will be correlated and the term with the correlation coefficient, ρ, can make a significant contribution to the error on a calculated value.

$y=mz%2Bc: \sigma^2_y=z^2\sigma^2_m%2B\sigma^2_c%2B2z\rho \sigma_m\sigma_c$

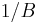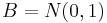In the special case of the inverse $1/B$ where $B=N(0,1)$ , the distribution is a Cauchy distribution and there is no definable variance. For such ratio distributions, there can be defined probabilities for intervals which can be defined either by Monte Carlo simulation, or, in some cases, by using the Geary-Hinkley transformation.^[2]

Example formulas

This table shows the variances of simple functions of the real variables 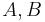$A,B\!$ , with standard deviations 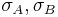$\sigma_A, \sigma_B\,$ , correlation coefficient 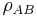$\rho_{AB}\,$ and precisely-known real-valued constants $a,b\,$ .

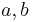Function	Variance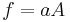
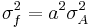
$f = aA\,$	$\sigma_f^2 = a^2\sigma_A^2$
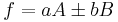
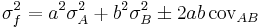
$f = aA \pm bB\,$	$\sigma_f^2 = a^2\sigma_A^2 %2B b^2\sigma_B^2\pm2ab\,\text{cov}_{AB}$
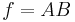
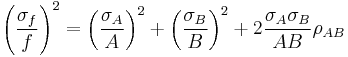
$f = AB\,$	$\left(\frac{\sigma_f}{f}\right)^2 = \left(\frac{\sigma_A}{A}\right)^2 %2B \left(\frac{\sigma_B}{B}\right)^2 %2B 2\frac{\sigma_A\sigma_B}{AB}\rho_{AB}$
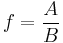
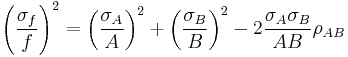
$f = \frac{A}{B}\,$	$\left(\frac{\sigma_f}{f}\right)^2 = \left(\frac{\sigma_A}{A}\right)^2 %2B \left(\frac{\sigma_B}{B}\right)^2 - 2\frac{\sigma_A\sigma_B}{AB}\rho_{AB}$
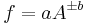
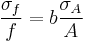
$f = aA^{\pm b}\,$	$\frac{\sigma_f}{f} = b \frac{\sigma_A}{A}$
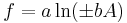
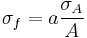
$f = a \ln(\pm bA)\,$	$\sigma_f = a \frac{\sigma_A}{A}$
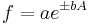
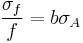
$f = a e^{\pm bA}\,$	$\frac{\sigma_f}{f} = b\sigma_A$
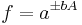
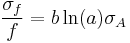
$f = a^{\pm bA}\,$	$\frac{\sigma_f}{f} = b\ln(a)\sigma_A$

For uncorrelated variables the covariance terms are zero. Expressions for more complicated functions can be derived by combining simpler functions. For example, repeated multiplication, assuming no correlation gives,

$f = AB(C); \left(\frac{\sigma_f}{f}\right)^2 = \left(\frac{\sigma_A}{A}\right)^2 %2B \left(\frac{\sigma_B}{B}\right)^2%2B \left(\frac{\sigma_C}{C}\right)^2.$

Partial derivatives

Given 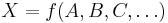$X=f(A, B, C, \dots)$

Absolute Error	Variance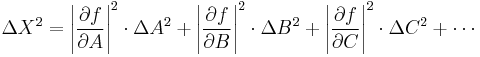
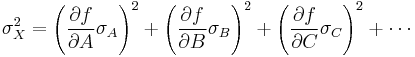$\Delta X^2=\left \|\frac{\partial f}{\partial A}\right \|^2\cdot \Delta A^2%2B\left \|\frac{\partial f}{\partial B}\right \|^2\cdot \Delta B^2%2B\left \|\frac{\partial f}{\partial C}\right \|^2\cdot \Delta C^2%2B\cdots$	$\sigma_X^2=\left (\frac{\partial f}{\partial A}\sigma_A\right )^2%2B\left (\frac{\partial f}{\partial B}\sigma_B\right )^2%2B\left (\frac{\partial f}{\partial C}\sigma_C\right )^2%2B\cdots$ ^[3]

Example calculation: Inverse tangent function

We can calculate the uncertainty propagation for the inverse tangent function as an example of using partial derivatives to propagate error.

Define

$f(x) = \arctan(x),$

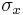where $\sigma_x$ is the absolute uncertainty on our measurement of $x$ .

The partial derivative of $f(x)$ with respect to $x$ is

$\frac{\partial f}{\partial x} = \frac{1}{1%2Bx^2}.$

Therefore, our propagated uncertainty is

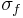$\sigma_{f} = \frac{\sigma_x}{1%2Bx^2},$

where $\sigma_f$ is the absolute propagated uncertainty.

Example application: Resistance measurement

A practical application is an experiment in which one measures current, I, and voltage, V, on a resistor in order to determine the resistance, R, using Ohm's law, 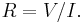$R = V / I.$

Given the measured variables with uncertainties, I±ΔI and V±ΔV, the uncertainty in the computed quantity, ΔR is

$\Delta R = \sqrt{\left|\Delta V\right|^2\left(\frac{1}{I}\right)^2%2B\left|\Delta I\right|^2\left(\frac{V}{I^2}\right)^2}.$

Notes

^ Leo Goodman (1960). "On the Exact Variance of Products". Journal of the American Statistical Association 55 (292): 708–713. doi:10.2307/2281592. JSTOR 2281592.
^ Jack Hayya, Donald Armstrong and Nicolas Gressis (July 1975). "A Note on the Ratio of Two Normally Distributed Variables". Management Science 21 (11): 1338–1341. doi:10.1287/mnsc.21.11.1338. JSTOR 2629897.
^ [|Vern Lindberg] (2009-10-05). "Uncertainties and Error Propagation" (in eng). Uncertainties, Graphing, and the Vernier Caliper. Rochester Institute of Technology. pp. 1. Archived from the original on 2004-11-12. http://web.archive.org/web/*/http://www.rit.edu/~uphysics/uncertainties/Uncertaintiespart2.html. Retrieved 2007-04-20. "The guiding principle in all cases is to consider the most pessimistic situation."

References

This has been a standard text used in undergraduate science and engineering for more than 40 years:

Bevington, P.R. and Robinson, D.K. (2002) Data Reduction and Error Analysis for the Physical Sciences, 3rd Ed., McGraw-Hill ISBN 0071199268

This text has detailed propagation-of-error material:

Meyer,S.L. (1975) Data Analysis for Scientists and Engineers, Wiley ISBN 0-471-59995-6

External links

A detailed discussion of measurements and the propagation of uncertainty explaining the benefits of using error propagation formulas and monte carlo simulations instead of simple significance arithmetic.
Uncertainties and Error Propagation, Vern Lindberg's Guide to Uncertainties and Error Propagation.
GUM, Guide to the Expression of Uncertainty in Measurement
EPFL An Introduction to Error Propagation, Derivation, Meaning and Examples of Cy = Fx Cx Fx'
uncertainties package, a program/library for transparently performing calculations with uncertainties (and error correlations).